BTreeAccess
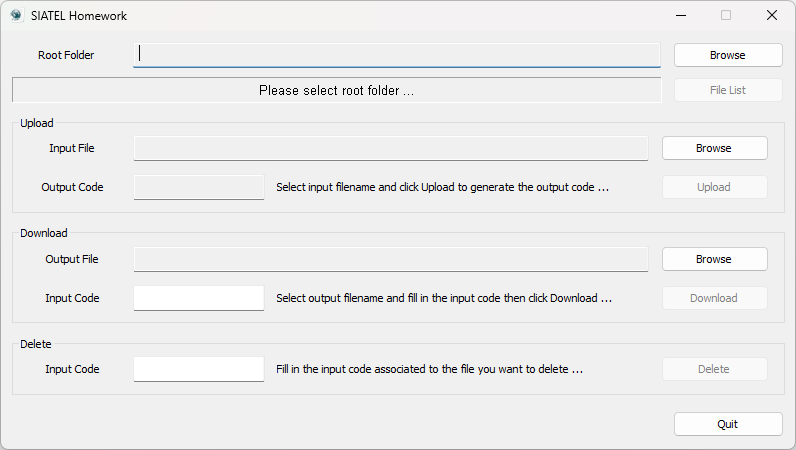
Introduction
Problem: Create a file server with optimal access to files, with the restriction that each folder can store N files maxim.
Solution: B-tree implementation.
Download source code: https://github.com/mihaimoga/BTreeAccess
Background
A B-tree is a method of placing and locating files (called records or keys) in a database. (The meaning of the letter B has not been explicitly defined.) The B-tree algorithm minimizes the number of times a medium must be accessed to locate a desired record, thereby speeding up the process.
B-trees are preferred when decision points, called nodes, are on hard disk rather than in random-access memory (RAM). It takes thousands of times longer to access a data element from hard disk as compared with accessing it from RAM, because a disk drive has mechanical parts, which read and write data far more slowly than purely electronic media. B-trees save time by using nodes with many branches (called children), compared with binary trees, in which each node has only two children. When there are many children per node, a record can be found by passing through fewer nodes than if there are two children per node. A simplified example of this principle is shown below.
In a tree, records are stored in locations called leaves. This name derives from the fact that records always exist at end points; there is nothing beyond them. The maximum number of children per node is the order of the tree. The number of required disk accesses is the depth. The image at the left shows a binary tree for locating a particular record in a set of eight leaves. The image at the right shows a B-tree of order three for locating a particular record in a set of eight leaves (the ninth leaf is unoccupied, and is called a null). The binary tree at the left has a depth of four; the B-tree at the right has a depth of three. Clearly, the B-tree allows a desired record to be located faster, assuming all other system parameters are identical. The tradeoff is that the decision process at each node is more complicated in a B-tree as compared with a binary tree. A sophisticated program is required to execute the operations in a B-tree. But this program is stored in RAM, so it runs fast.
In a practical B-tree, there can be thousands, millions, or billions of records. Not all leaves necessarily contain a record, but at least half of them do. The difference in depth between binary-tree and B-tree schemes is greater in a practical database than in the example illustrated here, because real-world B-trees are of higher order (32, 64, 128, or more). Depending on the number of records in the database, the depth of a B-tree can and often does change. Adding a large enough number of records will increase the depth; deleting a large enough number of records will decrease the depth. This ensures that the B-tree functions optimally for the number of records it contains.
The Theory
The algorithms for the search, create, and insert operations are shown below. Note that these algorithms are single pass; in other words, they do not traverse back up the tree. Since B-trees strive to minimize disk accesses and the nodes are usually stored on disk, this single-pass approach will reduce the number of node visits and thus the number of disk accesses. Simpler double-pass approaches that move back up the tree to fix violations are possible.
Since all nodes are assumed to be stored in secondary storage (disk) rather than primary storage (memory), all references to a given node will be preceeded by a read operation denoted by Disk-Read. Similarly, once a node is modified and it is no longer needed, it must be written out to secondary storage with a write operation denoted by Disk-Write. The algorithms below assume that all nodes referenced in parameters have already had a corresponding Disk-Read operation. New nodes are created and assigned storage with the Allocate-Node call. The implementation details of the Disk-Read, Disk-Write, and Allocate-Node functions are operating system and implementation dependent.
B-Tree-Search(x, k)
i <- 1
while i <= n[x] and k > keyi[x]
do i <- i + 1
if i <= n[x] and k = keyi[x]
then return (x, i)
if leaf[x]
then return NIL
else Disk-Read(ci[x])
return B-Tree-Search(ci[x], k)
The search operation on a B-tree is analogous to a search on a binary tree. Instead of choosing between a left and a right child as in a binary tree, a B-tree search must make an n-way choice. The correct child is chosen by performing a linear search of the values in the node. After finding the value greater than or equal to the desired value, the child pointer to the immediate left of that value is followed. If all values are less than the desired value, the rightmost child pointer is followed. Of course, the search can be terminated as soon as the desired node is found. Since the running time of the search operation depends upon the height of the tree, B-Tree-Search is O(logt n).
B-Tree-Create(T)
x <- Allocate-Node() leaf[x] <- TRUE n[x] <- 0 Disk-Write(x) root[T] <- x
The B-Tree-Create operation creates an empty B-tree by allocating a new root node that has no keys and is a leaf node. Only the root node is permitted to have these properties; all other nodes must meet the criteria outlined previously. The B-Tree-Create operation runs in time O(1).
B-Tree-Split-Child(x, i, y)
z <- Allocate-Node()
leaf[z] <- leaf[y]
n[z] <- t - 1
for j <- 1 to t - 1
do keyj[z] <- keyj+t[y]
if not leaf[y]
then for j <- 1 to t
do cj[z] <- cj+t[y]
n[y] <- t - 1
for j <- n[x] + 1 downto i + 1
do cj+1[x] <- cj[x]
ci+1 <- z
for j <- n[x] downto i
do keyj+1[x] <- keyj[x]
keyi[x] <- keyt[y]
n[x] <- n[x] + 1
Disk-Write(y)
Disk-Write(z)
Disk-Write(x)
If a node becomes "too full," it is necessary to perform a split operation. The split operation moves the median key of node x into its parent y where x is the ith child of y. A new node, z, is allocated, and all keys in x right of the median key are moved to z. The keys left of the median key remain in the original node x. The new node, z, becomes the child immediately to the right of the median key that was moved to the parent y, and the original node, x, becomes the child immediately to the left of the median key that was moved into the parent y.
The split operation transforms a full node with 2t – 1 keys into two nodes with t – 1 keys each. Note that one key is moved into the parent node. The B-Tree-Split-Child algorithm will run in time O(t) where t is constant.
B-Tree-Insert(T, k)
r <- root[T]
if n[r] = 2t - 1
then s <- Allocate-Node()
root[T] <- s
leaf[s] <- FALSE
n[s] <- 0
c1 <- r
B-Tree-Split-Child(s, 1, r)
B-Tree-Insert-Nonfull(s, k)
else B-Tree-Insert-Nonfull(r, k)
B-Tree-Insert-Nonfull(x, k)
i <- n[x]
if leaf[x]
then while i >= 1 and k < keyi[x]
do keyi+1[x] <- keyi[x]
i <- i - 1
keyi+1[x] <- k
n[x] <- n[x] + 1
Disk-Write(x)
else while i >= and k < keyi[x]
do i <- i - 1
i <- i + 1
Disk-Read(ci[x])
if n[ci[x]] = 2t - 1
then B-Tree-Split-Child(x, i, ci[x])
if k > keyi[x]
then i <- i + 1
B-Tree-Insert-Nonfull(ci[x], k)
To perform an insertion on a B-tree, the appropriate node for the key must be located using an algorithm similar to B-Tree-Search. Next, the key must be inserted into the node. If the node is not full prior to the insertion, no special action is required; however, if the node is full, the node must be split to make room for the new key. Since splitting the node results in moving one key to the parent node, the parent node must not be full or another split operation is required. This process may repeat all the way up to the root and may require splitting the root node. This approach requires two passes. The first pass locates the node where the key should be inserted; the second pass performs any required splits on the ancestor nodes.
Since each access to a node may correspond to a costly disk access, it is desirable to avoid the second pass by ensuring that the parent node is never full. To accomplish this, the presented algorithm splits any full nodes encountered while descending the tree. Although this approach may result in unnecessary split operations, it guarantees that the parent never needs to be split and eliminates the need for a second pass up the tree. Since a split runs in linear time, it has little effect on the O(t logt n) running time of B-Tree-Insert.
Splitting the root node is handled as a special case since a new root must be created to contain the median key of the old root. Observe that a B-tree will grow from the top.
B-Tree-Delete
Deletion of a key from a B-tree is possible; however, special care must be taken to ensure that the properties of a B-tree are maintained. Several cases must be considered. If the deletion reduces the number of keys in a node below the minimum degree of the tree, this violation must be corrected by combining several nodes and possibly reducing the height of the tree. If the key has children, the children must be rearranged. For a detailed discussion of deleting from a B-tree, refer to Section 19.3, pages 395-397, of Cormen, Leiserson, and Rivest or to another reference listed below.
The Practice
The main implementation is done in CNetworkHash class (SiatelHomeworkExt.h and SiatelHomeworkExt.cpp files) using hashmaps, as follows:
void RemoveAll()– removes all items from databaseBOOL ImportData()– loads database from a text configuration fileBOOL ExportData()– saves database to a text configuration fileint GenerateID()– generates a new key for insertionBOOL SearchItem(int nKey, int & nLevel, CString & strFilePath)– allows searching for a file into database, based on given keyBOOL UpdateItem(int nKey, int nLevel, CString strFilePath)– allows updating a file into database, based on given keyBOOL InsertItem(int nKey, int nLevel, CString strFilePath)– allows inserting a file into database, based on given keyBOOL DeleteItem(int nKey)– allows deleting a file from database, based on given key
CNetworkHash::CNetworkHash()
{
m_mapFileCode.InitHashTable(MAX_RANDOM_DATA);
m_mapFilePath.InitHashTable(MAX_RANDOM_DATA);
}
CNetworkHash::~CNetworkHash()
{
}
void CNetworkHash::RemoveAll()
{
m_listKey.RemoveAll();
m_mapFileCode.RemoveAll();
m_mapFilePath.RemoveAll();
}
BOOL CNetworkHash::ImportData()
{
int nLevel = 0, nFileCode = 0;
CString strFileLine, strFilePath;
const UINT nTextFileFlags = CFile::modeRead | CFile::typeText;
try {
CStdioFile pTextFile(GetFileList(), nTextFileFlags);
while (pTextFile.ReadString(strFileLine))
{
int nFirstNoLength = strFileLine.Find(_T(' '), 0);
int nSecondNoLength = strFileLine.Find(_T(' '), nFirstNoLength + 1);
ASSERT((nFirstNoLength >= 0) && (nSecondNoLength >= 0));
nFileCode = _tstoi(strFileLine.Mid(0, nFirstNoLength));
nLevel = _tstoi(strFileLine.Mid(nFirstNoLength + 1, nSecondNoLength));
strFilePath = strFileLine.Mid(nSecondNoLength + 1);
VERIFY(InsertItem(nFileCode, nLevel, strFilePath));
TRACE(_T("Importing data %d %d %s ...\n"), nFileCode, nLevel, strFilePath);
}
pTextFile.Close();
} catch (CFileException *pFileException) {
TCHAR lpszFileException[0x1000];
VERIFY(pFileException->GetErrorMessage(lpszFileException, 0x1000));
TRACE(_T("%s\n"), lpszFileException);
pFileException->Delete();
return FALSE;
}
return TRUE;
}
BOOL CNetworkHash::ExportData()
{
int nLevel = 0;
CString strFileLine, strFilePath;
const UINT nTextFileFlags = CFile::modeCreate | CFile::modeWrite | CFile::typeText;
try {
CStdioFile pTextFile(GetFileList(), nTextFileFlags);
const int nLength = GetSize();
for (int nIndex = 0; nIndex < nLength; nIndex++)
{
int nFileCode = GetKey(nIndex);
VERIFY(SearchItem(nFileCode, nLevel, strFilePath));
strFileLine.Format(_T("%d %d %s\n"), nFileCode, nLevel, strFilePath);
pTextFile.WriteString(strFileLine);
TRACE(_T("Exporting data %d %d %s ...\n"), nFileCode, nLevel, strFilePath);
}
pTextFile.Close();
} catch (CFileException *pFileException) {
TCHAR lpszFileException[0x1000];
VERIFY(pFileException->GetErrorMessage(lpszFileException, 0x1000));
TRACE(_T("%s\n"), lpszFileException);
pFileException->Delete();
return FALSE;
}
return TRUE;
}
int CNetworkHash::GenerateID()
{
int nLevel = 0;
CString strFilePath;
int nKey = GetNextID();
while (SearchItem(nKey, nLevel, strFilePath))
nKey = GetNextID();
return nKey;
}
BOOL CNetworkHash::SearchItem(int nKey, int & nLevel, CString & strFilePath)
{
BOOL bFileCode = m_mapFileCode.Lookup(nKey, nLevel);
BOOL bFilePath = m_mapFilePath.Lookup(nKey, strFilePath);
return (bFileCode && bFilePath);
}
BOOL CNetworkHash::UpdateItem(int nKey, int nLevel, CString strFilePath)
{
m_mapFileCode.SetAt(nKey, nLevel);
m_mapFilePath.SetAt(nKey, strFilePath);
return TRUE;
}
BOOL CNetworkHash::InsertItem(int nKey, int nLevel, CString strFilePath)
{
m_listKey.Add(nKey);
m_mapFileCode.SetAt(nKey, nLevel);
m_mapFilePath.SetAt(nKey, strFilePath);
return TRUE;
}
BOOL CNetworkHash::DeleteItem(int nKey)
{
int nOldLevel = 0, nNewLevel = 0;
CString strOldFilePath, strNewFilePath;
const int nLength = GetSize();
if (nLength > 0)
{
if (SearchItem(nKey, nNewLevel, strNewFilePath))
{
for (int nIndex = 0; nIndex < nLength; nIndex++)
{
if (nKey == m_listKey.GetAt(nIndex))
{
m_listKey.RemoveAt(nIndex);
break;
}
}
for (int nIndex = 0; nIndex < GetSize(); nIndex++)
{
const int nCurrentKey = m_listKey.GetAt(nIndex);
if (SearchItem(nCurrentKey, nOldLevel, strOldFilePath))
{
if (nOldLevel == GetSize())
{
CString strFileName = strNewFilePath;
// strNewFilePath = the file just deleted
// strOldFilePath = the file in the old location
strOldFilePath.Insert(0, GetRootFolder());
strFileName.Insert(0, GetRootFolder());
if (!MoveFile(strOldFilePath, strFileName))
{
const DWORD dwLastError = GetLastError();
CString strError = FormatLastError(dwLastError);
AfxMessageBox(strError, MB_OK | MB_ICONSTOP);
}
else
{
VERIFY(UpdateItem(nCurrentKey, nNewLevel, strNewFilePath));
}
break;
}
}
}
}
}
BOOL bFileCode = m_mapFileCode.RemoveKey(nKey);
BOOL bFilePath = m_mapFilePath.RemoveKey(nKey);
return (bFileCode && bFilePath);
}
Points of Interest
Given the above code, the upload, download and delete operations are implemented as follows:
void CSiatelHomeworkDlg::OnBnClickedUpload()
{
BOOL bCancelOperation = FALSE;
CString strMessage, strFilename;
CStringArray arrNetworkPath;
m_ctrlFolder.GetWindowText(m_strRootFolder);
if (m_strRootFolder.IsEmpty())
{
MessageBox(EMPTY_ROOT_FOLDER, _T("Error"), MB_OK);
}
else
{
if (USE_HASH_METHOD)
{
ASSERT(m_hashNetwork != NULL);
int nFileCode = m_hashNetwork->GenerateID();
int nPathCode = m_hashNetwork->GetSize();
CString strFileCode = m_hashNetwork->EncodeNetworkID(nFileCode);
CString strFilePath = m_hashNetwork->GetFilePath(nPathCode, arrNetworkPath);
VERIFY(m_hashNetwork->CreateNetworkPath(m_strRootFolder, arrNetworkPath));
strFilename.Format(_T("%s%s"), m_strRootFolder, strFilePath);
m_ctrlProgress.SetRange32(0, PROGRESS_RANGE);
m_ctrlProgress.SetPos(0);
m_ctrlProgress.ShowWindow(SW_SHOW);
if (!CopyFileEx(m_strInputFile, strFilename,
m_funcProgress, &m_ctrlProgress, &bCancelOperation, 0 ))
{
m_ctrlProgress.ShowWindow(SW_HIDE);
const DWORD dwLastError = GetLastError();
m_ctrlMessage.SetWindowText
(m_hashNetwork->FormatLastError(dwLastError));
}
else
{
VERIFY(m_hashNetwork->InsertItem(nFileCode, nPathCode, strFilePath));
strMessage.Format(_T("Done writing file %s [%s] ..."),
strFilename, strFileCode);
m_ctrlMessage.SetWindowText(strMessage);
m_ctrlOutputCode.SetWindowText(strFileCode);
m_ctrlProgress.SetPos(PROGRESS_RANGE-1);
m_ctrlProgress.UpdateWindow();
Sleep(SLEEP_INTERVAL);
m_ctrlProgress.ShowWindow(SW_HIDE);
}
}
else // USE B-TREE
{
}
}
}
void CSiatelHomeworkDlg::OnBnClickedDownload()
{
int nLevel = 0;
BOOL bCancelOperation = FALSE;
CString strMessage, strFilename;
CStringArray arrNetworkPath;
m_ctrlFolder.GetWindowText(m_strRootFolder);
if (m_strRootFolder.IsEmpty())
{
MessageBox(EMPTY_ROOT_FOLDER, _T("Error"), MB_OK);
}
else
{
if (USE_HASH_METHOD)
{
ASSERT(m_hashNetwork != NULL);
if (!m_hashNetwork->IsValidCode(m_strInputCode))
{
m_ctrlMessage.SetWindowText(INVALID_CHARS);
}
else
{
CString strFilePath; // relative path to file
int nFileCode = m_hashNetwork->DecodeNetworkID(m_strInputCode);
if (!m_hashNetwork->SearchItem(nFileCode, nLevel, strFilePath))
{
m_ctrlMessage.SetWindowText(FILE_DOES_NOT_EXISTS);
}
else
{
strFilename.Format(_T("%s%s"), m_strRootFolder, strFilePath);
m_ctrlProgress.SetRange32(0, PROGRESS_RANGE);
m_ctrlProgress.SetPos(0);
m_ctrlProgress.ShowWindow(SW_SHOW);
if (!CopyFileEx(strFilename, m_strOutputFile,
m_funcProgress, &m_ctrlProgress, &bCancelOperation, 0 ))
{
m_ctrlProgress.ShowWindow(SW_HIDE);
const DWORD dwLastError = GetLastError();
if (!m_hashNetwork->FileExists(strFilename))
m_ctrlMessage.SetWindowText(FILE_DOES_NOT_EXISTS);
else
m_ctrlMessage.SetWindowText
(m_hashNetwork->FormatLastError(dwLastError));
}
else
{
strMessage.Format(_T("Done reading file %s [%s] ..."),
strFilename, m_strInputCode);
m_ctrlMessage.SetWindowText(strMessage);
m_ctrlProgress.SetPos(PROGRESS_RANGE-1);
m_ctrlProgress.UpdateWindow();
Sleep(SLEEP_INTERVAL);
m_ctrlProgress.ShowWindow(SW_HIDE);
}
}
}
}
else // USE B-TREE
{
}
}
}
void CSiatelHomeworkDlg::OnBnClickedDelete()
{
int nLevel = 0;
CString strMessage, strFilename;
CStringArray arrNetworkPath;
m_ctrlFolder.GetWindowText(m_strRootFolder);
if (m_strRootFolder.IsEmpty())
{
MessageBox(EMPTY_ROOT_FOLDER, _T("Error"), MB_OK);
}
else
{
if (USE_HASH_METHOD)
{
ASSERT(m_hashNetwork != NULL);
if (!m_hashNetwork->IsValidCode(m_strDeleteCode))
{
m_ctrlMessage.SetWindowText(INVALID_CHARS);
}
else
{
CString strFilePath;
int nFileCode = m_hashNetwork->DecodeNetworkID(m_strDeleteCode);
if (!m_hashNetwork->SearchItem(nFileCode, nLevel, strFilePath))
{
m_ctrlMessage.SetWindowText(FILE_DOES_NOT_EXISTS);
}
else
{
strFilename.Format(_T("%s%s"), m_strRootFolder, strFilePath);
if (!m_hashNetwork->FileExists(strFilename))
{
m_ctrlMessage.SetWindowText(FILE_DOES_NOT_EXISTS);
}
else
{
if (!DeleteFile(strFilename))
{
const DWORD dwLastError = GetLastError();
m_ctrlMessage.SetWindowText
(m_hashNetwork->FormatLastError(dwLastError));
}
else
{
VERIFY(m_hashNetwork->DeleteItem(nFileCode));
strMessage.Format(_T("File %s
[%s] has been deleted ..."), strFilename, m_strDeleteCode);
m_ctrlMessage.SetWindowText(strMessage);
}
}
}
}
}
else // USE B-TREE
{
}
}
}
Works Cited
- Bayer, R., M. Schkolnick. Concurrency of Operations on B-Trees. In Readings in Database Systems (ed. Michael Stonebraker), pages 216-226, 1994.
- Cormen, Thomas H., Charles E. Leiserson, Ronald L. Rivest, Introduction to Algorithms, MIT Press, Massachusetts: 1998.
- Gray, J. N., R. A. Lorie, G. R. Putzolu, I. L. Traiger. Granularity of Locks and Degrees of Consistency in a Shared Data Base. In Readings in Database Systems (ed. Michael Stonebraker), pages 181-208, 1994.
- Kung, H. T., John T. Robinson. On Optimistic Methods of Concurrency Control. In Readings in Database Systems (ed. Michael Stonebraker), pages 209-215, 1994.