Introduction
The year 1998 was an important year for Web link analysis and Web search. Both the PageRank and the HITS algorithms were reported in that year. HITS was presented by Jon Kleinberg in January, 1998 at the Ninth Annual ACM-SIAM Symposium on Discrete Algorithms. PageRank was presented by Sergey Brin and Larry Page at the Seventh International World Wide Web Conference (WWW7) in April, 1998. Based on the algorithm, they built the search engine Google. The main ideas of PageRank and HITS are really quite similar. However, it is their dissimilarity that made a huge difference as we will see later. Since that year, PageRank has emerged as the dominant link analysis model for Web search, partly due to its query-independent evaluation of Web pages and its ability to combat spamming, and partly due to Google’s business success. In this article, we focus on PageRank.
PageRank relies on the democratic nature of the Web by using its vast link structure as an indicator of an individual page’s quality. In essence, PageRank interprets a hyperlink from page x to page y as a vote, by page x, for page y. However, PageRank looks at more than just the sheer number of votes or links that a page receives. It also analyzes the page that casts the vote. Votes casted by pages that are themselves "important" weigh more heavily and help to make other pages more "important". This is exactly the idea of rank prestige in social networks.
PageRank Algorithm
PageRank is a static ranking of Web pages in the sense that a PageRank value is computed for each page off-line and it does not depend on search queries. Since PageRank is based on the measure of prestige in social networks, the PageRank value of each page can be regarded as its prestige. We now derive the PageRank formula. Let us first state some main concepts again in the Web context.
In-links of page i: These are the hyperlinks that point to page i from other pages. Usually, hyperlinks from the same site are not considered.
Out-links of page i: These are the hyperlinks that point out to other pages from page i. Usually, links to pages of the same site are not considered.
From the perspective of prestige, we use the following to derive the PageRank algorithm:
- A hyperlink from a page pointing to another page is an implicit conveyance of authority to the target page. Thus, the more in-links that a page i receives, the more prestige the page i has.
- Pages that point to page i also have their own prestige scores. A page with a higher prestige score pointing to i is more important than a page with a lower prestige score pointing to i. In other words, a page is important if it is pointed to by other important pages.
According to rank prestige in social networks, the importance of page i (i’s PageRank score) is determined by summing up the PageRank scores of all pages that point to i. Since a page may point to many other pages, its prestige score should be shared among all the pages that it points to. Notice the difference from rank prestige, where the prestige score is not shared.
To formulate the above ideas, we treat the Web as a directed graph G =(V, E), where V is the set of vertices or nodes, i.e., the set of all pages, and E is the set of directed edges in the graph, i.e., hyperlinks. Let the total number of pages on the Web be n (i.e., n = |V|). The PageRank score of the page i (denoted by P(i)) is defined by P(i) = ∑(j,i)∈EP(j)/Oj where Oj is the number of out-links of page j. Mathematically, we have a system of n linear equations with n unknowns. We can use a matrix to represent all the equations. Let P be a n-dimensional column vector of PageRank values, i.e., P = (P(1), P(2), …, P(n))T.
Let A be the adjacency matrix of our graph with Aij=1/Oi if (i,j)∈E, 0 otherwise.
We can write the system of n equations with P=ATP.
This is the characteristic equation of the eigensystem, where the solution to P is an eigenvector with the corresponding eigenvalue of 1. Since this is a circular definition, an iterative algorithm is used to solve it. It turns out that if some conditions are satisfied (which will be described shortly), 1 is the largest eigenvalue and the PageRank vector P is the principal eigenvector. A well known mathematical technique called power iteration can be used to find P.
However, the problem is that equation P=ATP does not quite suffice because the Web graph does not meet the conditions. To introduce these conditions and the enhanced equation, let us derive the same equation P=ATP based on the Markov chain.
In the Markov chain model, each Web page or node in the Web graph is regarded as a state. A hyperlink is a transition, which leads from one state to another state with a probability. Thus, this framework models Web surfing as a stochastic process. It models a Web surfer randomly surfing the Web as a state transition in the Markov chain. Recall that we used Oi to denote the number of out-links of a node i. Each transition probability is 1/Oi if we assume the Web surfer will click the hyperlinks in the page i uniformly at random, the "back" button on the browser is not used and the surfer does not type in an URL. Let A be the state transition probability matrix, a square matrix of the following format: Aij represents the transition probability that the surfer in state i (page i) will move to state j (page j).
Given an initial probability distribution vector that a surfer is at each state (or page) p0 = (p0(1), p0(2), …, p0(n))T (a column vector) and an n*n transition probability matrix A, we have ∑i=1…np0 = 1, ∑j=1…nAij = 1.
Last equation is not quite true for some Web pages because they have no out-links. If the matrix A satisfies last equation, we say that A is the stochastic matrix of a Markov chain. Let us assume A is a stochastic matrix for the time being and deal with it not being that later.
In a Markov chain, a question of common interest is: Given the initial probability distribution p0 at the beginning, what is the probability that m steps/transitions later that the Markov chain will be at each state j? We can determine the probability that the system (or the random surfer) is in state j after 1 step (1 state transition) by using the following reasoning: p1(j) = ∑j=1…nAij(1)p0(i) where Aij(1) is the probability of going from i to j in 1 transition, and Aij(1) = Aij. We can write it with a matrix: p1=ATp0. In general, the probability distribution after k steps/transitions is: pk=ATpk-1.
By the Ergodic Theorem of Markov chains, a finite Markov chain defined by the stochastic transition matrix A has a unique stationary probability distribution if A is irreducible and aperiodic. These mathematical terms will be defined as we go along.
The stationary probability distribution means that after a series of transitions pk will converge to a steady-state probability vector π regardless of the choice of the initial probability vector p0, i.e., limk→∞pk = π. When we reach the steady-state, we have pk = pk+1 = π, and thus π=ATπ. π is the principal eigenvector of AT with eigenvalue of 1. In PageRank, π is used as the PageRank vector P. Thus, we again obtain the equation P=ATP.
Using the stationary probability distribution π as the PageRank vector is reasonable and quite intuitive because it reflects the long-run probabilities that a random surfer will visit the pages. A page has a high prestige if the probability of visiting it is high.
Now let us come back to the real Web context and see whether the above conditions are satisfied, i.e., whether A is a stochastic matrix and whether it is irreducible and aperiodic. In fact, none of them is satisfied. Hence, we need to extend the last equation to produce the "actual PageRank model". Let us look at each condition below.
First of all, A is not a stochastic (transition) matrix. A stochastic matrix is the transition matrix for a finite Markov chain whose entries in each row are non-negative real numbers and sum to 1. This requires that every Web page must have at least one out-link. This is not true on the Web because many pages have no out-links, which are reflected in transition matrix A by some rows of complete 0’s. Such pages are called the dangling pages (nodes).
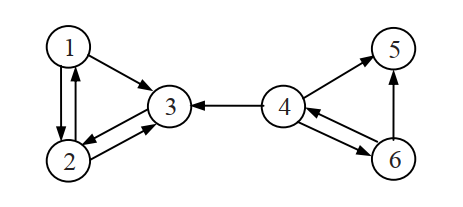
An example of a hyperlink graph
If we assume that the Web surfer will click the hyperlinks in a page uniformly at random, we have the following transition probability matrix:
[ 0 1/2 1/2 0 0 0 ] [1/2 0 1/2 0 0 0 ] [ 0 1 0 0 0 0 ] [ 0 0 1/3 0 1/3 1/3] [ 0 0 0 0 0 0 ] [ 0 0 0 1/2 1/2 0 ]
For example A12 = A13 = 1/2 because node 1 has two out-links. We can see that A is not a stochstic matrix because the fifth row is all 0’s, i.e., page 5 is a dangling page.
We can fix this problem in several ways in order to convert A to a stochastic transition matrix. We describe only two ways here:
- Remove those pages with no out-links from the system during the PageRank computation as these pages do not affect the ranking of any other page directly. Out-links from other pages pointing to these pages are also removed. After PageRanks are computed, these pages and hyperlinks pointing to them can be added in. Their PageRanks are easy to calculate based on equation P=ATP. Note that the transition probabilities of those pages with removed links will be slightly affected but not significantly.
- Add a complete set of outgoing links from each such page i to all the pages on the Web. Thus the transition probability of going from i to every page is 1/n assuming uniform probability distribution. That is, we replace each row containing all 0’s with e/n, where e is n-dimensional vector of all 1’s.
If we use the second method to make A a stochastic matrix by adding a link from page 5 to every page, we obtain
[ 0 1/2 1/2 0 0 0 ] [1/2 0 1/2 0 0 0 ] [ 0 1 0 0 0 0 ] [ 0 0 1/3 0 1/3 1/3] [1/6 1/6 1/6 1/6 1/6 1/6] [ 0 0 0 1/2 1/2 0 ]
Below, we assume that either one of the above is done to make A a stochastic matrix.
Second, A is not irreducible. Irreducible means that the Web graph G is strongly connected.
Definition (strongly connected): A directed graph G = (V, E) is strongly connected if and only if, for each pair of nodes u, v ∈ V, there is a path from u to v.
A general Web graph represented by A is not irreducible because for some pair of nodes u and v, there is no path from u to v. For example, in above figure, there is no directed path from node 3 to node 4. The adjustment in above matrix is not enough to ensure irreducibility. That is, in A , there is still no directed path from node 3 to node 4. This problem and the next problem can be dealt with using a single strategy (to be described shortly).
Finally, A is not aperiodic. A state i in a Markov chain being periodic means that there exists a directed cycle that the chain has to traverse.
Definition (aperiodic): A state i is periodic with period k > 1 if k is the smallest number such that all paths leading from state i back to state i have a length that is a multiple of k. If a state is not periodic (i.e., k = 1), it is aperiodic. A Markov chain is aperiodic if all states are aperiodic.
Below figure shows a periodic Markov chain with k = 3. The transition matrix is given on the left. Each state in this chain has a period of 3. For example, if we start from state 1, to come back to state 1 the only path is 1-2-3-1 for some number of times, say h. Thus any return to state 1 will take 3h transitions. In the Web, there could be many such cases.
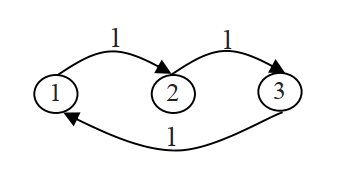
A periodic Markov chain with k = 3
It is easy to deal with the above two problems with a single strategy. We add a link from each page to every page and give each link a small transition probability controlled by a parameter d.
The augmented transition matrix becomes irreducible because it is clearly strongly connected. It is also aperiodic because the situation in last figure no longer exists as we now have paths of all possible lengths from state i back to state i. That is, the random surfer does not have to traverse a fixed cycle for any state. After this augmentation, we obtain an improved PageRank model. In this model, at a page, the random surfer has two options:
- With probability d, he randomly chooses an out-link to follow.
- With probability 1-d, he jumps to a random page without a link.
The following equation gives the improved model, P=((1-d)E/n+dAT)P, where E is eeT (e is a column vector of all 1’s) and thus E is a n*n square matrix of all 1’s. 1/n is the probability of jumping to a particular page. n is the total number of nodes in the Web graph. Note that this equation assumes that A has already been made a stochastic matrix.
(1-d)E/n+dAT is a stochastic matrix (but transposed). It is also irreducible and aperiodic as we discussed above. Here we use d = 0.9.
If we scale the last equation so that eTP = n, we obtain P=(1-d)e+dATP. Before scaling, we have eTP = 1 (i.e., P(1) + P(2) + … + P(n) = 1 if we recall that P is the stationary probability vector π of the Markov chain).
This gives us the PageRank formula for each page i as follows: P(i) = (1-d)+d∑j=1…nAjiP(j), which is equivalent to the formula given in the PageRank papers P(i) = (1-d)+d∑(j,i)∈EP(j)/Oj. The parameter d is called the damping factor which can be set to between 0 and 1, usually d = 0.85 is used.
The computation of PageRank values of the Web pages can be done using the well known power iteration method, which produces the principal eigenvector with the eigenvalue of 1. The algorithm is simple, and is given below. One can start with any initial assignments of PageRank values. The iteration ends when the PageRank values do not change much or converge. So, the iteration ends after the 1-norm of the residual vector is less than a pre-specified threshold ε. Note that the 1-norm for a vector is simply the sum of all the components.
PageRank-Iterate(G)
P0 ← e/n;
k ← 1;
repeat
Pk ← (1-d)e + dATPk-1;
k ← k + 1;
until ∥Pk – Pk-1∥1 < ε
return Pk;
Since we are only interested in the ranking of the pages, the actual convergence may not be necessary. Thus, fewer iterations are needed. In "Brin, S. and P. Lawrence. The anatomy of a large-scale hypertextual web search engine. Computer Networks, 1998", it is reported that on a database of 322 million links the algorithm converges to an acceptable tolerance in roughly 52 iterations.
Conclusion
The main advantage of PageRank is its ability to fight spam. A page is important if the pages pointing to it are important. Since it is not easy for Web page owner to add in-links into his/her page from other important pages, it is thus not easy to influence PageRank. Nevertheless, there are reported ways to influence PageRank. Recognizing and fighting spam is an important issue in Web search.
Another major advantage of PageRank is that it is a global measure and is query independent. That is, the PageRank values of all the pages on the Web are computed and saved off-line rather than at the query time. At the query time, only a lookup is needed to find the value to be integrated with other strategies to rank the pages. It is thus very efficient at the query time. Both these two advantages contributed greatly to Google’s success.
The main criticism is also the query-independence nature of PageRank. It could not distinguish between pages that are authoritative in general and pages that are authoritative on the query topic. Google may have other ways to deal with the problem, which we do not know due to the proprietary nature of the Google’s search algorithm. Another criticism is that PageRank does not consider time.
Finally, we note again that the link-based ranking is not the only strategy used in a search engine. Many other information retrieval methods, heuristics, and empirical parameters are also employed. However, their details are not published. We should also note that PageRank is not the only link-based static and global ranking algorithm. All major search engines, such as Bing and Yahoo!, have their own algorithms. Researchers also proposed other ranking methods that are not based on links, e.g., BrowseRank, which is based on a browsing graph built from the user search log.
